У сфері фінансів часто зустрічається таке поняття як «складний відсоток». Наприклад, банки пропонують своїм клієнтам розмістити вільні кошти на депозит із застосуванням складних відсотків. Що ж таке складний відсоток, як він його розрахувати та на скільки вигідніше розміщувати кошти під складний відсоток порівняно із звичайним відсотком?
Що таке складний відсоток?
Складний відсоток — це відсоток, що нараховується на початкову основну суму депозиту або кредиту, включаючи раніше нараховані відсотки.
Так як у схемі складних відсотків відбувається капіталізація (реінвестування) нарахованих відсотків, що призводить до постійного збільшення початкових вкладень, то часто таку схему називають “відсоток на відсотки”.
З використанням схеми простих відсотків нараховані відсотки не капіталізуються, тому простий відсоток нараховується лише початкову суму вкладень. Відповідно, при однаковому розмірі відсоткової ставки приріст вкладень відбувається швидше у разі застосування складного відсотка.
Формула складних відсотків
Складні відсотки можна розрахувати за наведеною нижче формулою:

Коментар за формулою розрахунку складних відсотків:
- відсоткову ставку використовують у вигляді десяткового дробу, тобто. початковий розмір відсоткової ставки необхідно розділити на 100. Наприклад, якщо відсоткова ставка дорівнює 12% річних, то формулі необхідно використовувати значення 0,12;
- n – це число, яке приводить у відповідність відсоткову ставку до періодичності нарахувань. Якщо відсотки нараховуються щорічно, то значення n дорівнює 1; якщо раз на півроку, то n дорівнює 2; якщо раз на квартал, то n дорівнює 4; якщо щомісяця, то n дорівнює 12 (наприклад, розділивши річну відсоткову ставку на 12 ми отримаємо щомісячну відсоткову ставку).
- nt – це загальна кількість періодів нарахування складних відсотків. Наприклад, якщо вклад розміщено на 3 роки з щомісячною капіталізацією відсотків, то загальна кількість періодів нарахувань складе 36 періодів (12*3).
Приклад розрахунку складних відсотків
Припустимо, що вкладник відкрив у банку депозитний рахунок на 100 тис. дол. під 3% річних терміном на 3 роки з щомісячною капіталізацією відсотків. Визначимо суму, яку банк виплатить вкладнику після закінчення терміну дії депозитного договору.
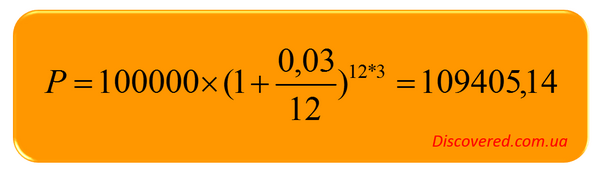
Отже, вкладник отримає 109405,14 дол. після закінчення терміну дії депозитного договору, у тому числі сума нарахованих відсотків становитиме 9405,14 дол. Якби для нарахування використовувалися прості відсотки, то вкладник отримав лише 9000 дол, тобто. різниця становитиме 405,14 дол.
У формулі складних відсотків кінцевий результат залежить від рівня відсоткової ставки та періодичності капіталізації відсотків. Що розмір процентної ставки і чим більше періодів капіталізації, то більшою буде кінцева цифра. І навпаки. Так, якби у наведеному вище прикладі капіталізація відсотків відбувалася не щомісяця, а щорічно, то підсумкова цифра становила б 109272,70 дол. Залежність підсумкової суми вкладу від періодичності капіталізації відсотків проілюстрована нижче.
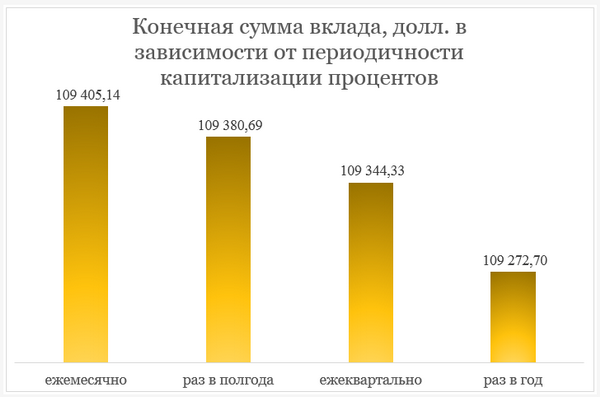
Слід розрізняти поняття “нарахування відсотків” та “капіталізація відсотків”. Так, у депозитному договорі може бути передбачено, що нарахування відсотків банк здійснює щодня, але капіталізація відсотків (тобто приєднання до тіла депозиту для подальшого нарахування відсотків) здійснюється щомісяця чи кварталу.


